祖源计算器中的Fst分布密度之统计学意义初探
继一下这两篇文章:
https://www.wegene.com/question/25090
https://www.wegene.com/question/25246
我们对祖源计算器中的Fst分布密度使用matlab的分布拟合器进行了统计学上的分析以发现分布密度函数(PDF)
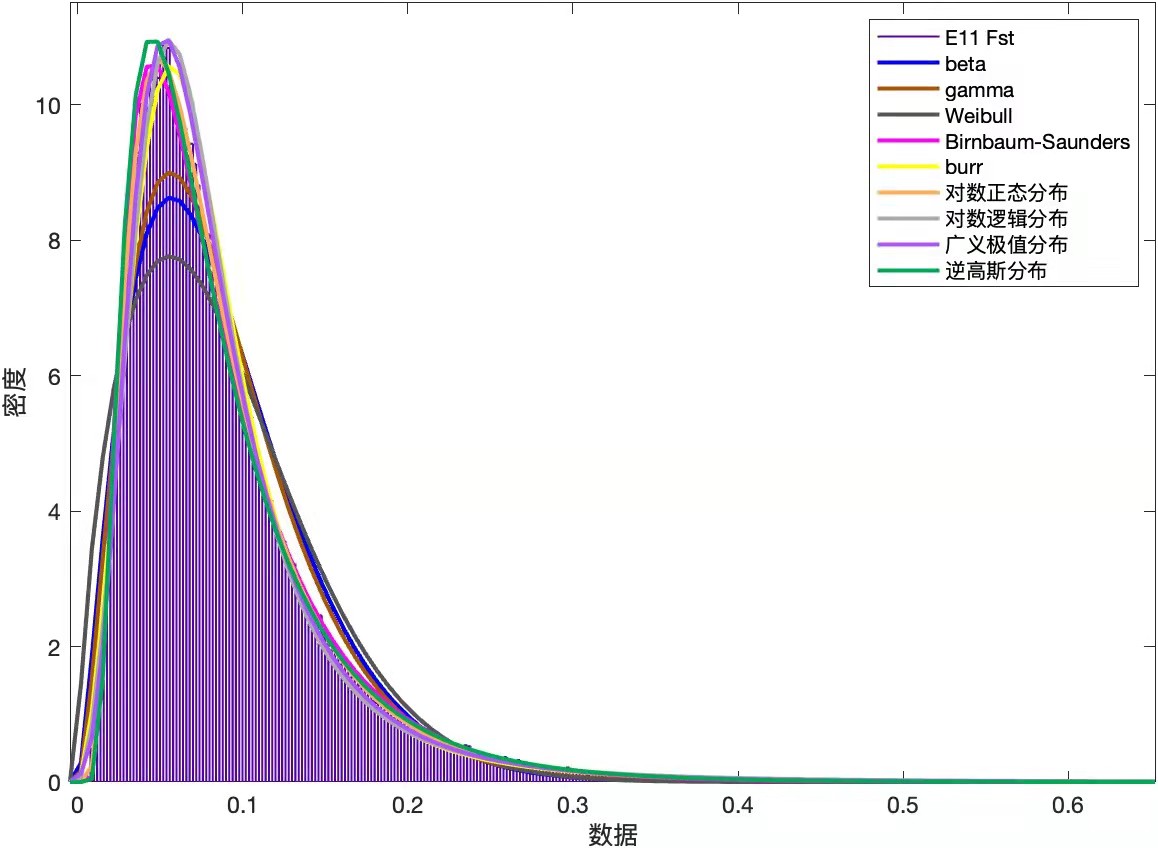
首先以e11为入手点筛选出来哪些分布函数能比较好的拟合e11这个计算器。效果如图一(过于离谱的结果已经被排除了)
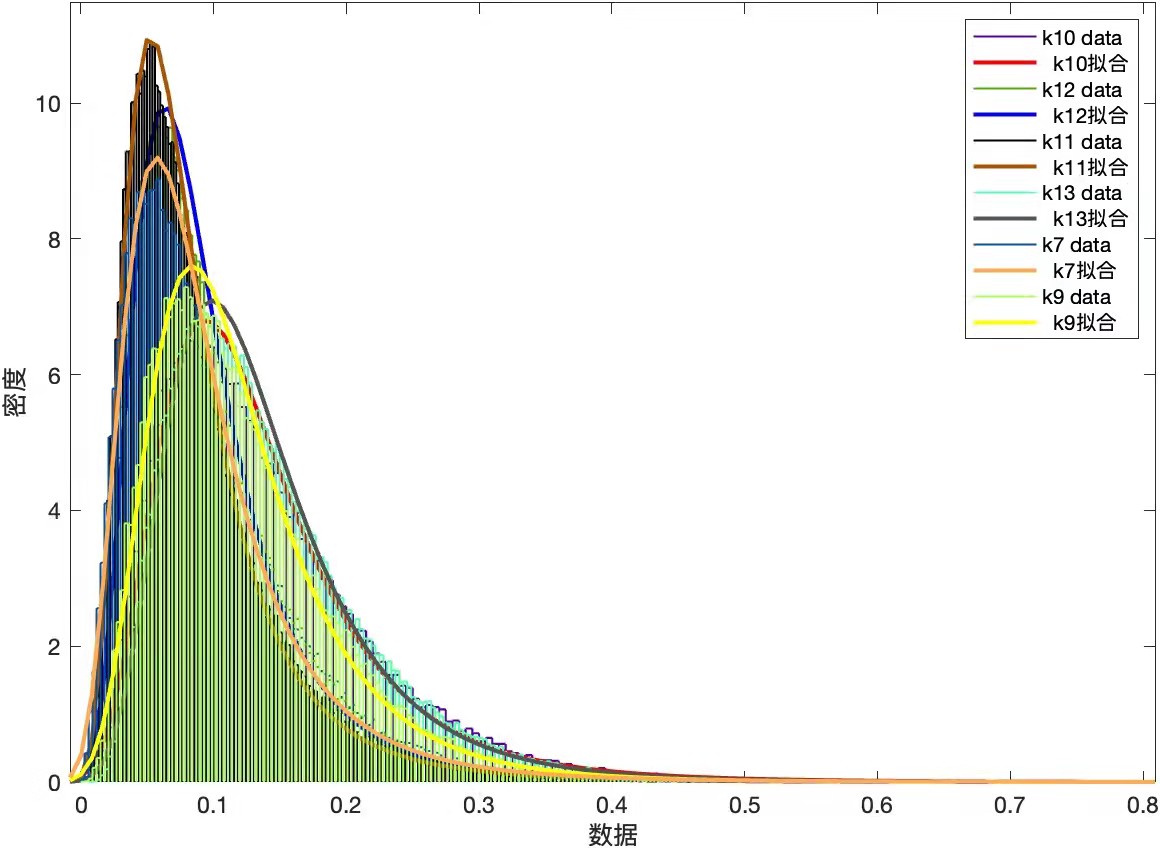
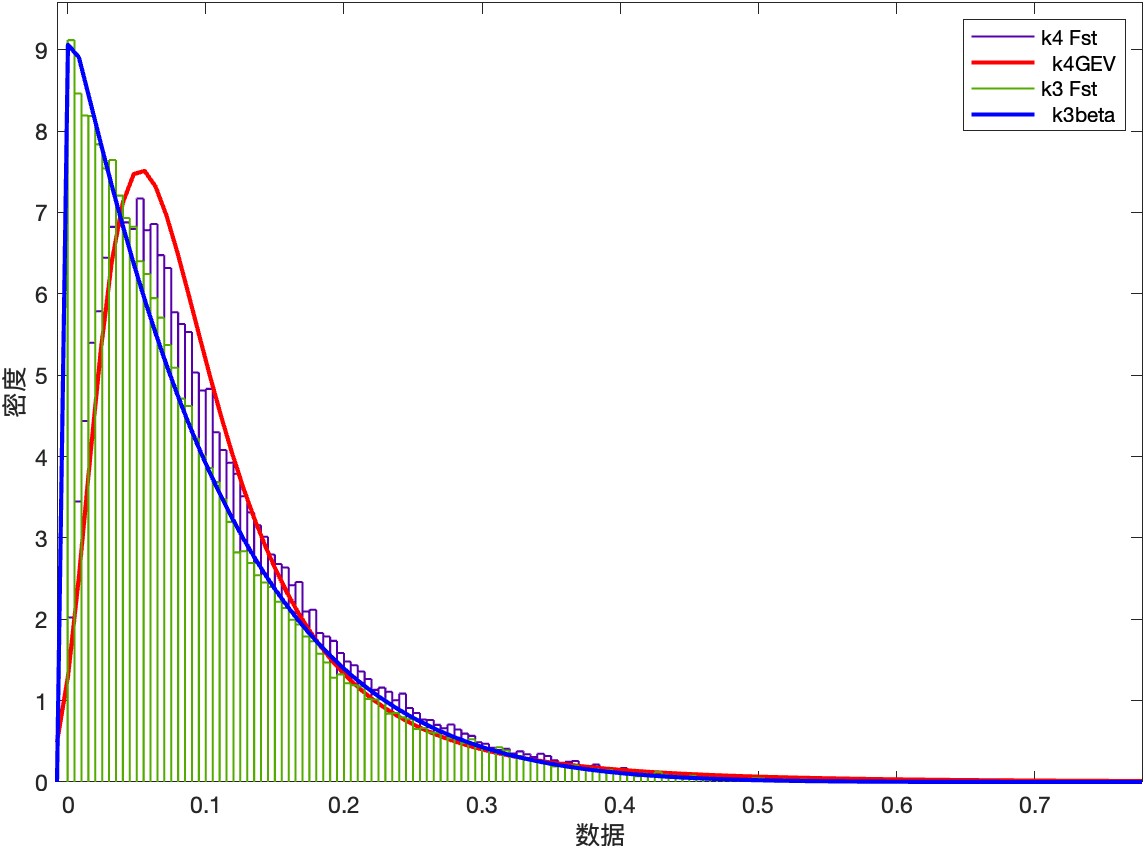
之后,分别用筛选出来的几个分布函数拟合其他k值的计算器,筛选出可以在不同k值下都能(或大部分)比较好拟合的分布函数。效果如图二(其他不符合的均被排除,图中所显示的是广义极值分布)
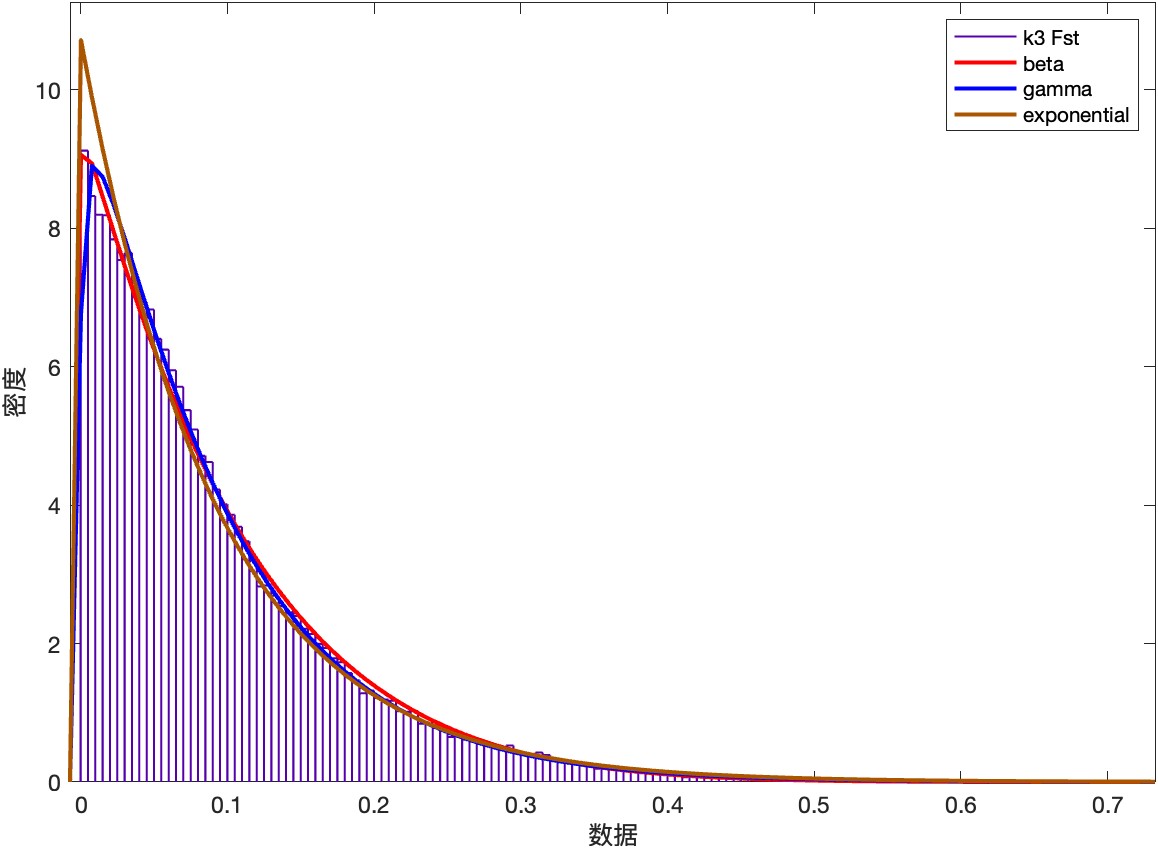
接着,我们将三个梯度k值(以k取3,12和47为例)发现低k值组还是不能很好的拟合。于是我们再用其他的分布密度函数对小k值的Fst分布密度进行拟合,进行筛选,发现在k值为3时,beta函数能较好的拟合。如下图所示:
最后,我们简单的对拟合出的系数进行分析。我们首先观察到广义极值函数中有系数k是否为0的两种情况。如下图所示:
而通过拟合,无论在何计算器k值时,广义极值函数的系数k均不为0,所以我们抹去广义极值函数中系数k为0的情况以简化函数。并且由k值为3向上递增观察密度函数形状,发现当k值为4时密度函数变为广义极值函数形状。所以确定确定了两函数的使用条件。合并并简化后得到如下图所示的经验公式:
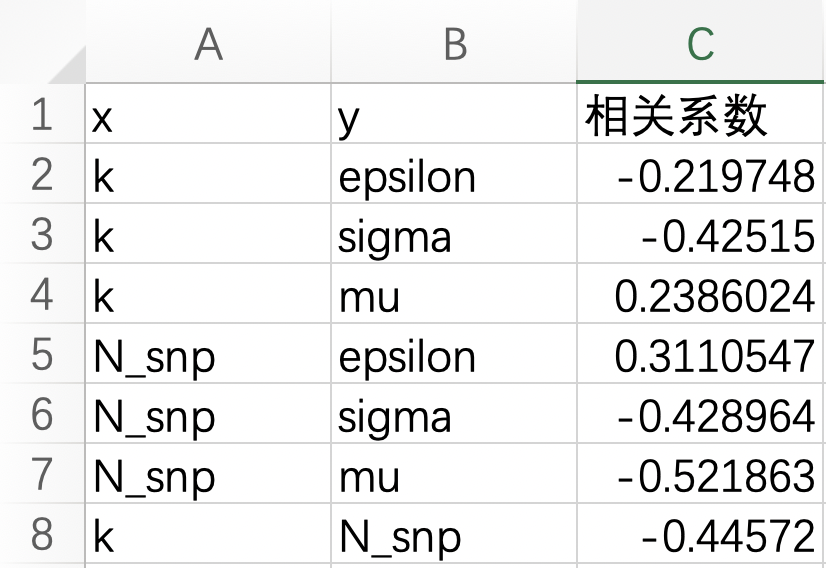
另外,通过计算自变量与因变量间的相关系数(如下表),我们确定k与系数sigma和mu以及计算器snp数与sigma和mu之间均呈负相关,并且通过计算相关系数的绝对值并比较大小以及k与snp数程负相关(因为两量间相关系数也为负)可知,很有可能是k值首先影响计算器snp数,再间接影响两系数的。当然这里都是猜测,具体还需要进一步研究才能确定。
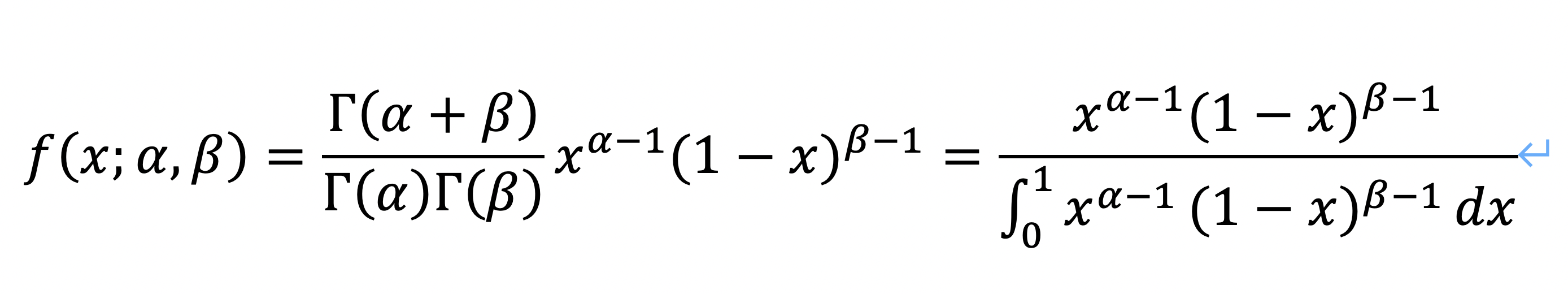
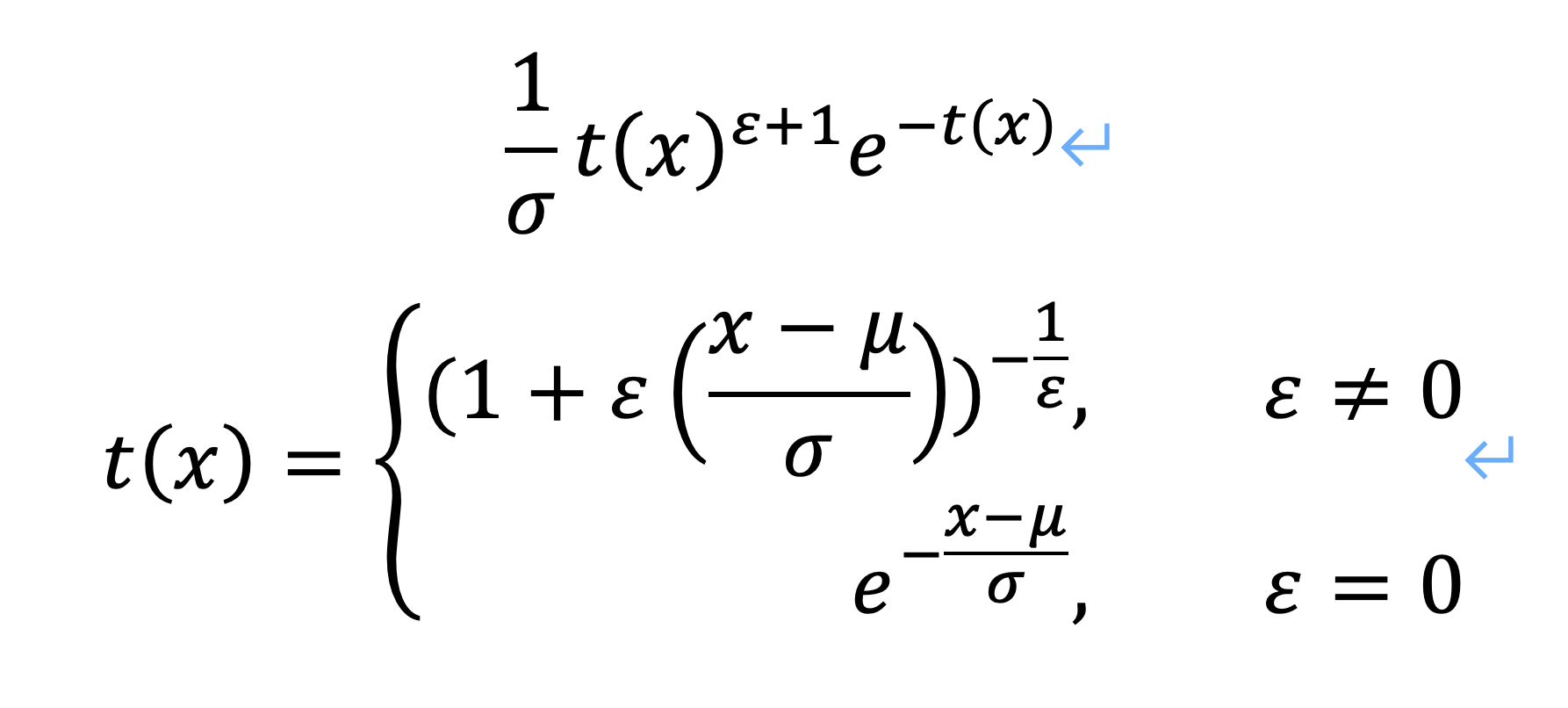
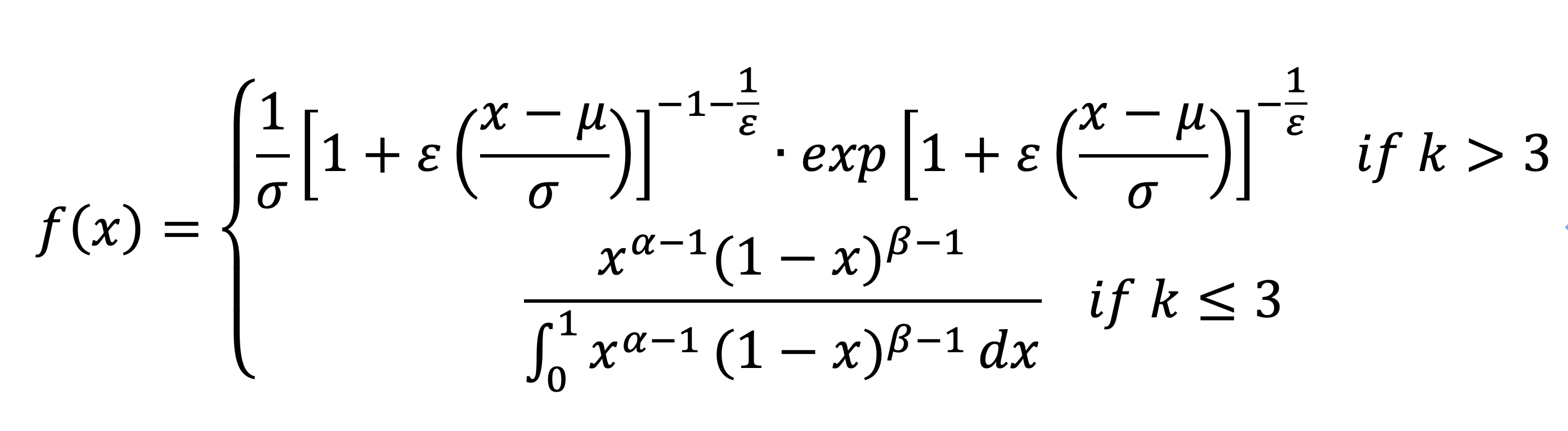


2 个回复
赞同来自:
赞同来自:
要回复问题请先登录或注册